【医療者向け】R統計でおすすめのパッケージ3選【研究者が語る】

京極真

本記事では「臨床で働いています。Rで統計解析したいのですが、おすすめのパッケージはありますか？」という疑問にお答えします

なぜRで統計解析なの？

Rで統計解析する利点は、コストゼロでさまざまな課題に対応できるようになるところにあります。

Rはヘルスケア領域でであうほとんどすべての問題に対応できるため、使いこなせるようになるメリットはめっちゃ大きいです。

臨床研究で必要なことは何でもできるようになりますから、スキルアップをかねて習得すべしです。

「Rで統計解析を学ぶにはどうするの？」という疑問をお持ちの方は以下の記事をご参照ください。

動画で効率よく学ぶことができますよ。

以下の記事では、２本の動画について詳しく解説しています。

Rのパッケージってなに？

パッケージとは、国内外にいるRユーザーが開発したRの機能を拡張するためのプログラムです。

パッケージはすべて無料でして、R単独でインストールしたり、アンインストールしたりできます。

パッケージはCRAN（Comprehensive R Archive Network）というネットワークから入手することができます。

その手順はとても簡単です。

まず、Rstudioのpackageのinstallをクリックします（赤でかこったところをクリック）。

すると、install packagesというボックスがでるので、インストールしたいパッケージ名を記載し、installをクリックしたらOKです（赤でかこったところをクリック）。

別の方法としては、hogeをインストールしたい場合は、scriptに　install.packages("hoge")　と書いて実行したらOKです。

パッケージのアンインストールは、scriptに　remove.packages("hoge")　を記載してから実行したらOKです。

医療系の方々におすすめの統計モデルの特徴

医療者におすすめの統計モデルの特徴は以下の通りです。

ヘルスケア領域は疾病・障害の評価と治療の他に生活支援を行うものでして、こうした課題は人間・環境・生活行為のダイナミックでインタラクティブなプロセスとして発生します。

統計解析するときは、この複雑な事象を単純化しないとダメです。

けど、あまりに単純化すると、ヘルスケア領域であつかっている事象からかけ離れたものになります。

実証するためにシンプルな仮説を立てつつも、ある程度そこにヘルスケア領域らしさをのせたい。

以下では、そういう希望に応えうるR統計パッケージをさくっと紹介しますが、おすすめのパッケージは多数ありまして、そのすべてを書くと読みにくくなるので、本記事では3つだけ紹介します。

医療者におすすめのR統計パッケージ

構造方程式モデル：lavaan

構造方程式モデルは因子分析、回帰分析、パス解析などの機能を統合した手法であり、めちゃくちゃ柔軟にデータ解析することができます。

インストールは　install.packages("lavaan")　と書いて実行するだけです。

例えば、通常の回帰分析は説明変数は複数OKですが、目的変数は1つのみです。

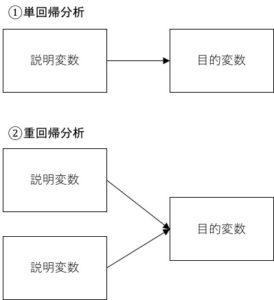
でも、構造方程式モデルならば、上記の単回帰や重回帰に加えて、それらでは不可能だった説明変数も目的変数も複数の仮説でもOKになります。

以下には単純な例を示していますが、もっと複雑な仮説でもあつかえます。

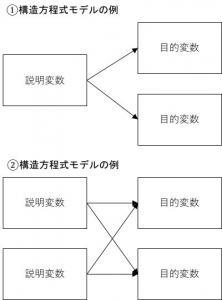
例えば、ケアがADLとQOLに与える影響を同時に検証することも可能です。

また、構造方程式モデルは直接測定したデータ（観測変数）から、実際には測定していない変数（潜在変数）を作り、その関係性を検証することができます。

例えば、QOLは関節可動域などのような物理量をもっておらず、直接測定することはできません。

なので、QOLを問ういくつかの質問項目に解答（観測変数）していただき、その得点からQOLという直接測定できない変数（潜在変数）を推論することになります。

ヘルスケア領域にはQOLのほかに、アドヒアランス、意志決定などたくさんの潜在変数があります。

これらに適切に対応した統計解析を行うには、構造方程式モデルが不可欠です。

構造方程式モデルに対応したRパッケージは複数ありますが、lavaanがおすすめです。

ぜひ使ってみるとよいです。

ベイズ構造方程式モデル：blavaan

blavaanはlavaanのベイズ推定版です。

推定法はデータに統計モデルを当てはめる方法です。

lavaanの推定法は最小二乗法、最尤推定法などです。

それに対して、blavaanはベイズ推定法に対応しています。

「最小二乗法、最尤推定法 vs ベイズ推定法」という説明がなされることがありますが、これはちょっとミスリーディングです。

これらは対立するものではなく、推定法に与えられた制約の違いだと理解しておくとよいです。

制約は「最小二乗法→最尤推定法→ベイズ推定法」の順に緩くなり、それにともなって扱えるデータや統計モデルが増えていきます。

blavaanは構造方程式モデルにベイズ推定法の利点をもちこめます。

blavaanはJAGSあるいはStanというベイズ専用のソフトを使うので、事前にそれらのインストールを行います（もちろん無料）。

デフォルトではJAGSを使用しますが、MCMCをまわすときに　taget="stan"　と指定することでStanで計算することができます。

次に、install.packages("blavaan")　と書いて実行してblavaanをインストールするだけです。

一般化線形混合モデル：brms

一般化線形混合モデルは、回帰分析、t検定、分散分析、共分散分析、対数線形モデルなどの機能を統合した手法であり、固定効果と変量効果を組み合わせることによって個体差や場所差など対象の個性を科学することができます。

インストールは　install.packages("brms")　と書いて実行するだけです。

例えば、単回帰分析を使って年齢から体重を予測するとしましょう。

単回帰分析は　y = ax +b　で表しますので、yは体重、xは年齢になって、前提として傾きaと切片bは全対象者で共通していると仮定することになります。

すると、結果によっては例えば、対象者が100名いたら全員が1ヶ月で2キロ増える、という解釈になったりします。

でもこれは普通に考えるとかなり不自然です。

体重の増加の程度は人によって異なるからです。

それに対して、一般化線形混合モデルならば、傾きaと切片bは対象者によって異なるというような個体差を考慮した統計モデルを組めるので、対象者による体重の増減の違いを扱えます。

つまり、一般化線形混合モデルは、治療の効果の出方には個人差があるということを考慮したうえで計算できるわけです。

一般化線形混合モデルは「線形モデル→一般化線形モデル→一般化線形混合モデル→階層ベイズモデル」という発展に位置づけることができます。

一般化線形混合モデルは最尤推定法とベイズ推定法で使うことができます。

最尤推定法で用いるときは一般化線形混合モデル、ベイズ推定法で用いるときは階層ベイズモデルの一種としての一般化線形混合モデルに位置づけられます。

brmsはベイズ推定法で一般化線形混合モデルを運用するものであり、マルコフ連鎖モンテカルロ法で推定値を計算する階層ベイズモデルの一種であると言えます。

最尤推定法で一般化線形混合モデルを行いたいときは　install.packages("lmerTest")　と書いてパッケージをインストールすればよいです。

ただ、一般化線形混合モデルはモデルが複雑なので最尤推定法で計算するのはしんどいので、基本的にはbrmsを使うとよいです。

まとめ：【医療者向け】R統計でおすすめのパッケージ3選【研究者が語る】

本記事では「臨床で働いています。Rで統計解析したいのですが、おすすめのパッケージはありますか？」という疑問にお答えしました。

本記事ではlavaan、blavaan、brmsを紹介しましたが、他にもヘルスケア領域でおすすめのパッケージはあります。

また別の記事で紹介できたらと思います。

また、統計を学びたい人むけの書籍については以下の記事に詳しく紹介しています。ぜひ、どうぞ！！

京極　真

Ph.D.、OT

TwitterFacebookInstagramYouTubeContact

1976年大阪府生まれ。Ph.D、OT。Thriver Project代表。吉備国際大学ならびに同大学大学院・教授。作業療法学科長、保健科学研究科長、（通信制）保健科学研究科長。首都大学東京大学院人間健康科学研究科博士後期課程・終了。『医療関係者のための信念対立解明アプローチ』『作業療法リーズニングの教科書』『作業で創るエビデンス』など著書・論文多数。